LIMITES DE UNA FUNCION
↞Limites
de una función↠
El limite en una función es la indeterminación de la ecuación, es decir, es la proximidad que tiene esta de ser completa o igualada a A.
Se dice que una función f(x) tiene como limite L, en el punto X = A, si es posible aproximar f(x) a L, tanto como quiera cuando X se acerca indefinidamente a A, siendo distinto de A. Dado el punto a y según la anterior definición, existen dos formas de aproximar X a A desde valores X > A (por la derecha) y desde valores X < A (por la izquierda). En cada uno de los casos se obtienen valores denominados limite por la derecha (X>A+) Y limite por la izquierda (X<A-). Por definición, para que exista dos limites laterales (por la derecha y por izquierda). Se expresa como:
LIM F(X)= L ⇔ ∃ LIM F(X) y LIM f(x),siendo LIM F(X) = LIM F(X)= L
x➝a+ x➝a- x➝a+ x➝a-

CARACTERÍSTICAS DE UN LIMITE:
ESTE DEBE SER IGUALADO POR EL LIMITE (X⟶?), SI AL HACER LAS OPERACIONES CORRESPONDIENTES DA COMO RESULTADO 0, LA FUNCIÓN ESTA DEBE SER REALIZADA PARA ENCONTRAR EL NUMERO O INTERSECCIÓN DE LAS FUNCIONES.
*PASO A PASO PARA RESOLVER LIMITES
1.Identifica si la ecuación esta al máximo simplificada, de no ser así, identificar que método usaras.
LIM X²-9 = (3)²-9 = 0
x⟶3 X-3 3-3 = 0
2. Factoriza usando cualquier método para factorizar como son
-Factor común, diferencia de cuadrados, binomio cuadrado perfecto, Ax² +Bx +C, entre otros.
LIM (X + 3)(X - 3)= ⟶ binomio al cuadrado perfecto
x⟶3 X - 3
3. Al encontrar dos binomios multiplicándose y dividiéndose sobre uno igual se cancelan. NOTA: no olvides que el lugar donde se elimina el binomio que se encuentra solo le corresponde un 1.
LIM (X + 3) 1= ⟶ se simplifico
x⟶3 1
4. Después de haber factorizar y simplificar la ecuaciones podemos sustituir la equis por el limite correspondiente.
LIM= (3)+ 3 = 6 ⟶ Resultado
ASINTOTAS VERTICALES Y HORIZONTALES
Si una función f(x) crece indefinidamente cuando el valor de la variable X tiende a A, se dice que su límite es infinito +∞ si el crecimiento es en sentido positivo, y -∞, si lo es en sentido negativo). También es posible definir límites de una función cuando el valor de X tiende a +∞ o a -∞.
Asintota vertical o función F(X) = A


Asintota horizontal o función F(X) = B
LIMITES INFINITOS
La solución de limites infinitos o indeterminados es mas difícil que los determinados, ya que este depende de una constantes ∞.
REGLAS:
* SUMAR O RESTAR INFINITO:
* MULTIPLICACION DE INFINITOS
* REGLA DE SIGNOS
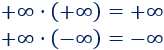
* DIVIDIR ENTRE INFINITO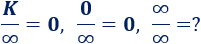
* DIVIDIR ENTRE CERO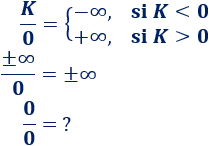
PASO A PASO DE COMO RESOLVER CUANDO UN LIMITE TIENDE A ∞EJEMPLO: 1
1. Reducir o simplificar la ecuación a lo máximo.
LIM 2X + 2 = 2(X + 1))= ⟶ Factor común
X⟶∞ X + 1 X + 1
2. Ya que la ecuación esta factorizada y simplificada, se eliminan los binomios iguales.
LIM 2 (1) = 2 ⟶ En este caso la X fue eliminada y no
X⟶∞ 1 se puede sustituir la x, el resultado
es 2.
3. Sustituir la ecuación.
EJEMPLO: 2
1. Reducir o simplificar la ecuación a lo máximo.
LIM X = ⟶ En este caso no se puede factorizar
X⟶∞ 12
2. Ya que la ecuación esta factorizada y simplificada, se eliminan los binomios iguales.
3. Sustituir la ecuacion.
LIM ∞ = ∞ ⟶ Al sustituir la ecuacion el infinito 12 quedo arriba y como la regla lo dice si un infinito queda arriba de una constante (K) el resultado es ∞
Se dice que una función f(x) tiene como limite L, en el punto X = A, si es posible aproximar f(x) a L, tanto como quiera cuando X se acerca indefinidamente a A, siendo distinto de A. Dado el punto a y según la anterior definición, existen dos formas de aproximar X a A desde valores X > A (por la derecha) y desde valores X < A (por la izquierda). En cada uno de los casos se obtienen valores denominados limite por la derecha (X>A+) Y limite por la izquierda (X<A-). Por definición, para que exista dos limites laterales (por la derecha y por izquierda). Se expresa como:
LIM F(X)= L ⇔ ∃ LIM F(X) y LIM f(x),siendo LIM F(X) = LIM F(X)= L
x➝a+ x➝a- x➝a+ x➝a-
↞PROPIEDADES DE LOS LIMITES⇸
Dadas dos funciones f(x) y g(x) que tiene limite en un punto a se cumplen las siguientes propiedades:
о El limite de la suma de ambas funciones es igual a la suma de los limites .
о El limite de la diferencia se calcula como la diferencia
о El límite del producto de las funciones es igual al producto de sus límites.
о El límite del cociente entre ambas funciones es igual al cociente entre los límites, siempre y cuando el límite del denominador sea distinto de cero.
о El límite del producto de una constante por una función viene determinado por la multiplicación de la constante por el límite de la función.
CARACTERÍSTICAS DE UN LIMITE:
ESTE DEBE SER IGUALADO POR EL LIMITE (X⟶?), SI AL HACER LAS OPERACIONES CORRESPONDIENTES DA COMO RESULTADO 0, LA FUNCIÓN ESTA DEBE SER REALIZADA PARA ENCONTRAR EL NUMERO O INTERSECCIÓN DE LAS FUNCIONES.
*PASO A PASO PARA RESOLVER LIMITES
1.Identifica si la ecuación esta al máximo simplificada, de no ser así, identificar que método usaras.
LIM X²-9 = (3)²-9 = 0
x⟶3 X-3 3-3 = 0
2. Factoriza usando cualquier método para factorizar como son
-Factor común, diferencia de cuadrados, binomio cuadrado perfecto, Ax² +Bx +C, entre otros.
LIM (X + 3)(X - 3)= ⟶ binomio al cuadrado perfecto
x⟶3 X - 3
3. Al encontrar dos binomios multiplicándose y dividiéndose sobre uno igual se cancelan. NOTA: no olvides que el lugar donde se elimina el binomio que se encuentra solo le corresponde un 1.
LIM (X + 3) 1= ⟶ se simplifico
x⟶3 1
4. Después de haber factorizar y simplificar la ecuaciones podemos sustituir la equis por el limite correspondiente.
LIM= (3)+ 3 = 6 ⟶ Resultado
Si una función f(x) crece indefinidamente cuando el valor de la variable X tiende a A, se dice que su límite es infinito +∞ si el crecimiento es en sentido positivo, y -∞, si lo es en sentido negativo). También es posible definir límites de una función cuando el valor de X tiende a +∞ o a -∞.
Asintota vertical o función F(X) = A
Asintota horizontal o función F(X) = B
La solución de limites infinitos o indeterminados es mas difícil que los determinados, ya que este depende de una constantes ∞.
REGLAS:
* SUMAR O RESTAR INFINITO:

* MULTIPLICACION DE INFINITOS
* REGLA DE SIGNOS
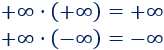
* DIVIDIR ENTRE INFINITO
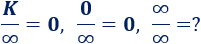
* DIVIDIR ENTRE CERO
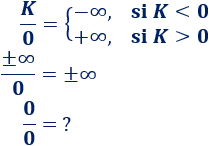
PASO A PASO DE COMO RESOLVER CUANDO UN LIMITE TIENDE A ∞EJEMPLO: 1
1. Reducir o simplificar la ecuación a lo máximo.
LIM 2X + 2 = 2(X + 1))= ⟶ Factor común
X⟶∞ X + 1 X + 1
2. Ya que la ecuación esta factorizada y simplificada, se eliminan los binomios iguales.
LIM 2 (1) = 2 ⟶ En este caso la X fue eliminada y no
X⟶∞ 1 se puede sustituir la x, el resultado
es 2.
3. Sustituir la ecuación.
EJEMPLO: 2
1. Reducir o simplificar la ecuación a lo máximo.
LIM X = ⟶ En este caso no se puede factorizar
X⟶∞ 12
2. Ya que la ecuación esta factorizada y simplificada, se eliminan los binomios iguales.
3. Sustituir la ecuacion.
LIM ∞ = ∞ ⟶ Al sustituir la ecuacion el infinito 12 quedo arriba y como la regla lo dice si un infinito queda arriba de una constante (K) el resultado es ∞
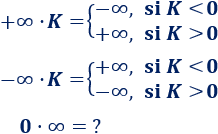

Comentarios
Publicar un comentario